引用:https://www.google.co.jp/webhp?sourceid=chrome-instant&ion=1&espv=2&ie=UTF-8#q=z%E3%82%B9%E3%82%B3%E3%82%A2%E3%81%A8%E3%81%AF
Zスコア データ群の当該数値から平均値を引いて、標準偏差で割ることで求めます。
これにより、このデータ群は平均が0、標準偏差が1になり、
単位が異なる数値も比較することが可能となります。 このような変換を標準化や基準化とも言われ、
変換した数値のことをZスコアと呼ばれます。
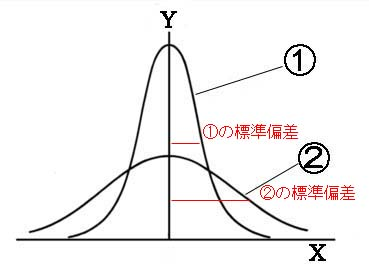
Zスコアのイメージ図
引用:http://www.u-gakugei.ac.jp/~kishilab/z-score.htm
①の分布も②の分布も、左右対称かつ平均値・中央値・最頻値が一致しており、
X軸に漸近しているので正規分布です。
しかし、このままでは①と②の単純な比較はできません。
例えば①が国語のテスト、②が数学のテストだったとします。
国語も数学も60点だったとしたら、どっちが嬉しいでしょうか。
①のテストの60点ラインを見てみましょう。 このラインより右側は面積が小さくなっています。
つまり、60点以上を取った人が少ないテストだったわけです。
②のテストの60点ラインを見てみましょう。 このラインより右側は①のものに比べ、
面積が大きくなっています。 つまり、60点以上を取った人は結構いるんですね。
よって、国語の60点の方が嬉しい、となります。
しかし、見た目ではこれ以上の判断はできません。
これを数値的に表現するために標準化を行います。
①の標準偏差と②の標準偏差が違うので、二つのグラフは重なりません。
標準化とは、①と②の標準偏差を同じ長さにすることです。つまり同じ比率にしてしまうのです。
こうして、平均値が0、標準偏差が1である正規分布を描きます。
この正規分布のことを標準正規分布と呼びます。
次式で求めます。
z=(取った得点-平均点)/標準偏差
この式によると、平均点と同じ点数だと0になることがよくわかると思います。
こうして得られた得点がz得点です。
──────────自分の考え
Zスコアは、異なった標準偏差曲線(ベルカーブ)を
世間一般で言われていた偏差値の計算式は、Z=50+10×(取った得点-平均点)/標準偏差
ですので、偏差値として再計算すれば、下記のようになります。
数値を正しく評価することができなくとも、偏差値と聞けば50より大きいのが能力が有ると、
おぼろげながら、私でさえイメージできます。
プロフィットファクターだけでは評価できません。
あるていど様子を見て、成績評価が○以上のもを残し、×は退場ということになります。
以前は学生の能力を表す数値として一般化されていましたが、学力偏重と称し、
廃止されるやむなきに至りました。
、、、が、学生の時のゆとり教育などは、社会になってからの競争社会にいきなり放り込まれることになり、
全くの温室育ちから、いきなりの弱肉強食になりますから、学生時代から競争社会であったほうが、
自分自身のためになるのかなと思います。
| 201605 | |||||||
| ストラテジー | PF |
|
シャープレシオ | Z-スコア | 偏差値 | 評価 | |
| 01 | 0.62 | -0.19 | 0.37 | 53.7 | ○ | ||
| 02 | 0.94 | -0.01 | 4.96 | 99.6 | ◎ | ||
| 03 | 1.58 | 0.07 | -0.60 | 44.0 | × | ||
| 04 | |||||||
| 05 | 0.52 | 0.33 | 1.40 | 64.0 | ○ | ||
| 06 | 0.59 | -0.26 | -1.64 | 33.6 | × | ||
| 07 | 1.41 | 0.09 | -1.98 | 30.2 | × | ||
| 08 | 0.73 | -0.04 | 0.35 | 83.7 | ◎ | ||
| 09 | 0.91 | -0.04 | 0.02 | 50.2 | △ | ||
| 10 | 2.67 | 0.47 | -0.99 | 40.1 | × | ||
| 11 | 1.07 | 0.04 | -0.55 | 44.5 | × | ||
| 12 | 0.18 | -0.16 | -1.95 | 30.5 | × | ||
| 21 | 1.22 | 0.06 | 0.36 | 53.6 | ○ | ||
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
コメントを残す